容量过程建模实例
基本概念
使用机理分析法进行建模。
数学模型: 指过程在各输入量的作用下,其相应输出量变化的函数关系数学表达式。
通道: 输入量与输出量间的信号联系
自衡:对象受到干扰作用后,平衡状态被破坏,无须外加任何控制作用,依靠对象本身自动平衡的倾向,逐渐地达到新的平衡状态的性质,称为平衡能力。
容量
阻力
一、单容过程
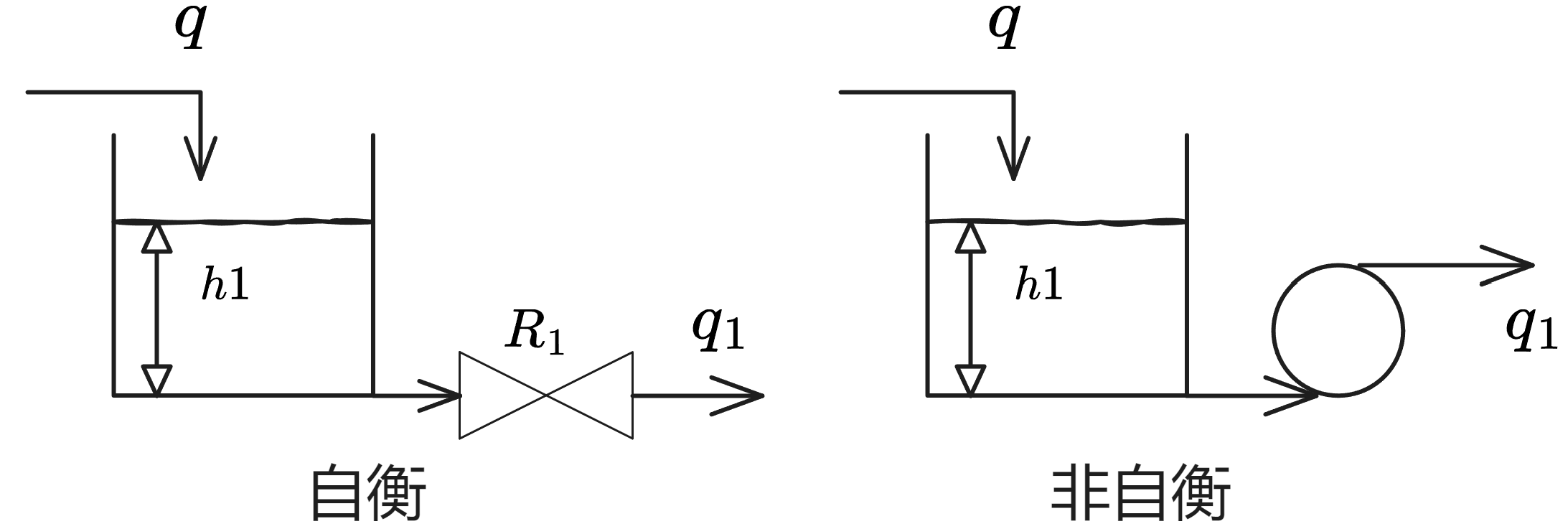
自衡
无自衡
抽水泵
二、多容过程
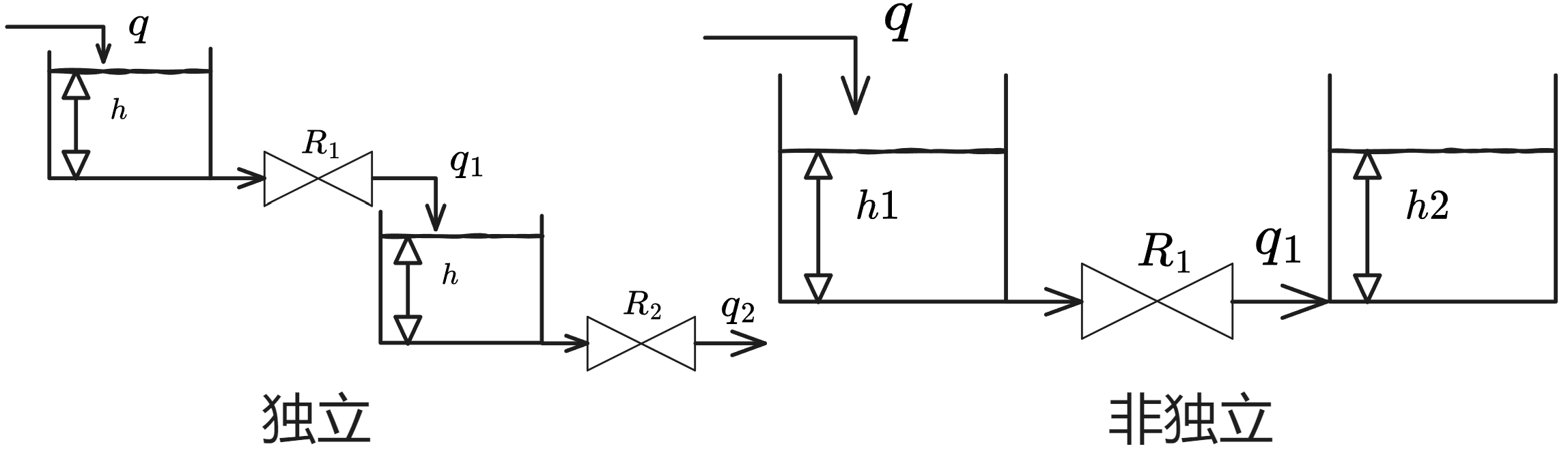
独立
也即单容过程的简单组合
非独立
实际的例题(组合)
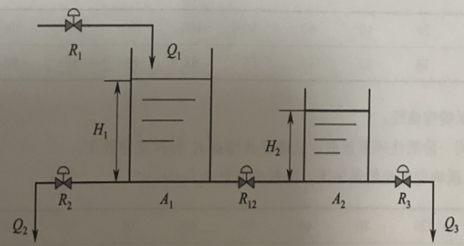
使用机理分析法进行建模。
数学模型: 指过程在各输入量的作用下,其相应输出量变化的函数关系数学表达式。
通道: 输入量与输出量间的信号联系
自衡:对象受到干扰作用后,平衡状态被破坏,无须外加任何控制作用,依靠对象本身自动平衡的倾向,逐渐地达到新的平衡状态的性质,称为平衡能力。
容量
阻力

抽水泵

也即单容过程的简单组合
